量子计算的核心逻辑在于通过特定操作增加目标解的振幅（或概率）。在前文中，我们利用辅助量子比特实现了对特定状态的“踢回”操作，从而将目标状态与其他状态区分开来。然而，这种操作仅涉及相位翻转，并未提升目标状态的概率。因此，如何增大目标状态的概率成为量子计算求解的关键步骤。

基于此，量子计算过程可以划分为两步：预示（Oracle）和扩散（Diffusion）。

• 预示步骤用于识别目标解；
• 扩散步骤用于累积并放大目标解的振幅。

Grover 算法提供了一种常见的扩散实现方法，其核心思想可以用“镜像操作”来理解。对于一个双量子比特系统，经初始化后具有四种均匀状态：

\ket{\psi}=\frac{1}{2}(\ket{00}+\ket{01}+\ket{10}+\ket{11})

其振幅向量为：

\ket{\psi}=\frac{1}{2}\begin{bmatrix}1\\1\\1\\1\end{bmatrix}

以状态为横坐标，振幅为纵坐标绘图有：

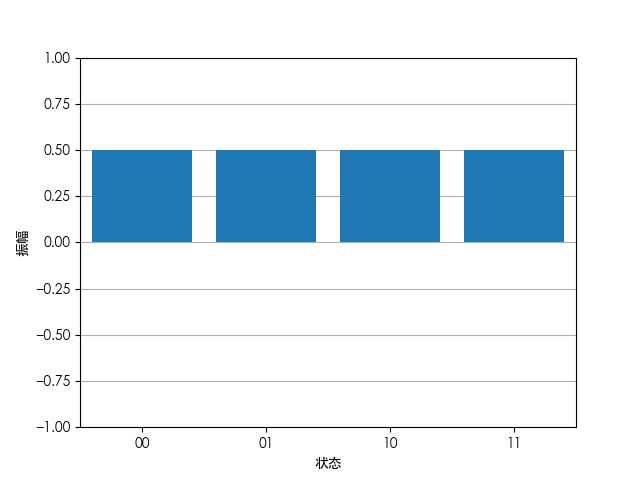
若待查找的解为 00，经过预示操作的相位翻转后状态为：

\ket{\psi^{\prime}}=\frac{1}{2}\begin{bmatrix}-1\\1\\1\\1\end{bmatrix}

即：

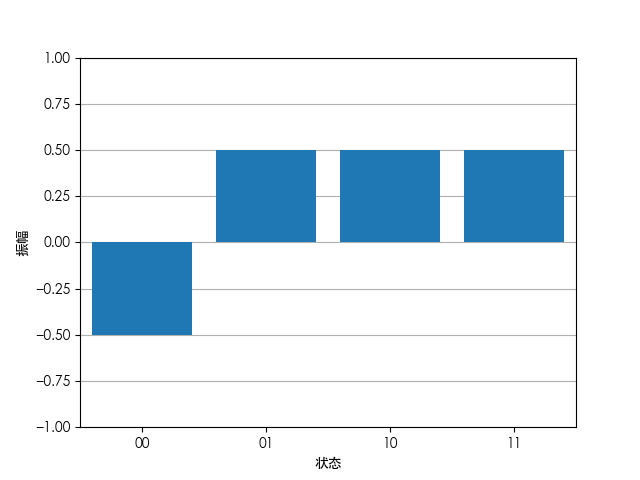
若以原状态的平均振幅为对称轴，翻转预示后状态，即以图中红色虚线翻转各状态概率：

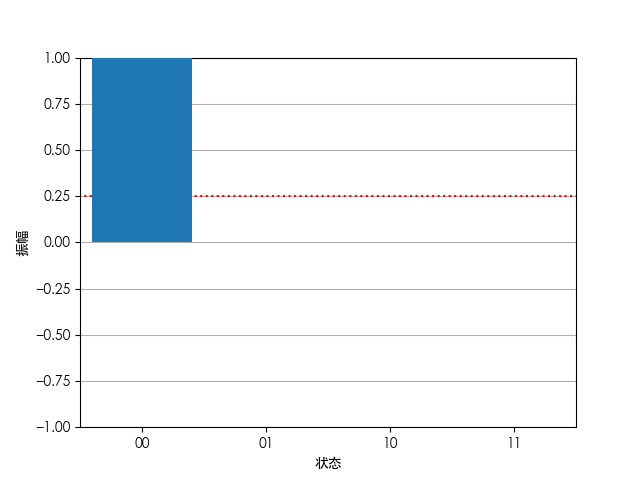
可发现，目标状态振幅扩大为 1，而其余状态的振幅均减至 0，该对称操作可写为算符形式：

2\ket{\psi}\bra{\psi}-I

该操作将非目标状态振幅相对于平均值“压低”，而目标状态振幅被“抬高”。对于多量子比特系统，初始振幅更小，因此需要多次迭代“预示 + 镜像”操作，以累积目标解的振幅，提高测量时获得目标状态的概率，其最优迭代次数 R 有：

R \approx \frac{\pi}{4} \sqrt{N}

即，对于 N 个量子比特的均匀初始态，其时间复杂度为：

O(\sqrt{N})

相比于经典查找算法（复杂度为 N），Grover 算法具有明显优势。

注意到对称操作中存在加减，无法直接在量子计算机上实现，因此需化简该算符。对于初始状态为均匀分布的 2 量子比特系统，有：

2\ket{\psi}\bra{\psi}-I = H^{\otimes2} (2\ket{00} \bra{00}  - I)H^{\otimes2}

其中，只需实现：

2\ket{00} \bra{00}  - I = \begin{bmatrix} 1 &0&0&0\\0&-1&0&0\\0&0&-1&0\\0&0&0&-1\end{bmatrix}

考虑到全局相位，可写为：

2\ket{00} \bra{00}  - I \propto \begin{bmatrix} -1 &0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}

即当且仅当 0、1 号量子比特为 00 时，对一个辅助量子比特进行相位翻转操作，从而实现对控制量子位的条件相位操作。用量子门表示为：

2\ket{00}\bra{00} - I = X^{\otimes 2} \, CCZ \, X^{\otimes 2}

其中，CCZ 门作用在两个控制比特（原来的 0、1 号量子比特）和一个额外的辅助比特上，完成条件相位翻转。

对于多量子比特系统，这一结构可以推广：使用若干个 X 门和多比特受控 Z 门实现条件相位操作。最终，Grover 算法的扩散算符可以表示为：

2\ket{\psi}\bra{\psi} - I = H^{\otimes n} \, X^{\otimes n} \, C^nZ \, X^{\otimes n} \, H^{\otimes n}