Bloch 球(Bloch Sphere)是一个几何化的工具,用于直观表示单个量子比特的状态。它把量子态映射到一个单位球的表面,这样就能便捷的观察量子态变化。为了便于理解单量子操作门的功能,这里我们通过 Bloch 球来说明这些操作。
三维极坐标系
在传统的笛卡尔坐标系中,一个点由 (x, y, z) 三个坐标确定。而在三维极坐标系中,点的位置由半径 r 和两个角度 θ, φ 决定:
(r, \theta, \phi), \quad 0 \le \theta \le \pi,\ 0 \le \phi < 2\pi
其中:
- r 为点到原点的距离;
- θ 为极角(polar angle),点与 z 轴之间的夹角;
- φ 为方位角(azimuthal angle),点在 x-y 平面上的投影与 x 轴的夹角。
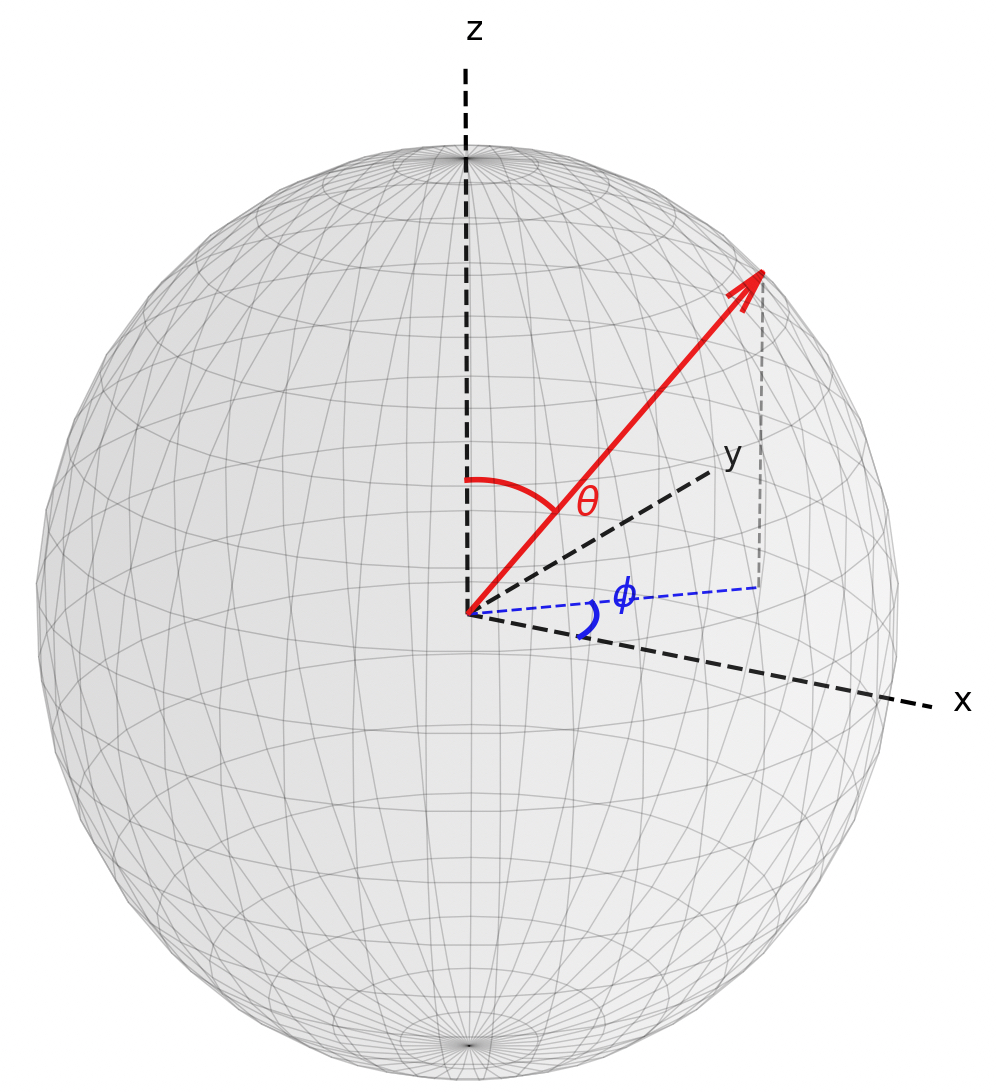
因此,不难得出,从极坐标到笛卡尔坐标有:
\begin{cases}
x = r \sin\theta \cos\phi\\
y = r \sin\theta \sin\phi\\
z = r \cos\theta
\end{cases}反向转换有:
\begin{cases}
r = \sqrt{x^2 + y^2 + z^2}\\
\theta = \arccos\left(\dfrac{z}{r}\right)\\
\phi = \arctan2(y,x)
\end{cases}参数的几何意义
根据三维极坐标系,知:
- r 决定点距离原点的远近;
- θ 决定点的位置沿 z 轴的倾斜程度;
- φ 决定点在水平面(x-y 平面)上的方向。
因此,如果把点固定在单位球面上(r=1),那么任何一个点的位置就完全由 θ 和 φ 唯一决定。
Bloch 球
在量子计算中,任意单量子比特状态可表示为:
\ket{\psi} = \alpha \ket{0} + \beta \ket{1}其中:
\alpha, \beta \in \mathbb{C}, \quad |\alpha|^2 + |\beta|^2 = 1根据复数的极坐标表示形式有:
\alpha = |\alpha|\, e^{i\varphi_\alpha}, \quad \beta = |\beta|\, e^{i\varphi_\beta}因此:
\ket{\psi} = |\alpha|\, e^{i\varphi_\alpha} \ket{0} + |\beta|\, e^{i\varphi_\beta} \ket{1}因为量子态乘以一个全局相位因子后的量子态与原量子态在物理上完全等价,意味着可以任意选择一个合适的全局相位因子 γ 简化表达式,而不改变任何可测量的物理结果,这里选择:
\gamma = -\varphi_\alpha
则有:
\begin{aligned}
\ket{\psi'}
&= e^{-i\varphi_\alpha} \ket{\psi} \\
&= e^{-i\varphi_\alpha}
\left( |\alpha| e^{i\varphi_\alpha} \ket{0}
+ |\beta| e^{i\varphi_\beta} \ket{1} \right) \\
&= \left( |\alpha| e^{i\varphi_\alpha} e^{-i\varphi_\alpha} \right) \ket{0}
+ \left( |\beta| e^{i\varphi_\beta} e^{-i\varphi_\alpha} \right) \ket{1} \\
&= |\alpha| \ket{0}
+ \left( |\beta| e^{i(\varphi_\beta-\varphi_\alpha)} \right) \ket{1} \\
\end{aligned}令:
\phi=\varphi_\beta-\varphi_\alpha
则:
\ket{\psi'} = |\alpha| \ket{0} + |\beta| e^{i \phi} \ket{1}根据归一化条件:
|\alpha|^2 + |\beta|^2 = 1
可令:
\begin{cases}
|\alpha| = \cos\!\left(\frac{\theta}{2}\right) \\
|\beta| = \sin\!\left(\frac{\theta}{2}\right)
\end{cases}则有:
\ket{\psi'} = \cos\!\left(\frac{\theta}{2}\right) \ket{0} + e^{i \phi} \sin\!\left(\frac{\theta}{2}\right) \ket{1}这意味着任意单量子比特状态都可以唯一映射到 Bloch 球上的一点,其中 (θ,φ) 即该点的极坐标。
量子门操作
旋转算符
对于绕任意轴 n 旋转角度 θ 的算符可通过矩阵指数函数定义:
R_{n}(\theta) = e^{-i \frac{\theta}{2} \, \hat{\sigma}_{n}}其中,
\hat{\sigma}_{n} = n_{x} \, \hat{\sigma}_{x} + n_{y} \, \hat{\sigma}_{y} + n_{z} \, \hat{\sigma}_{z}自反算符
对于算符 A,若其满足
A^2 = I
则称其为自反算符。
对于任意算符 X,根据泰勒级数展开(Taylor Series Expansion),有:
e^{X}
= \sum_{n=0}^{\infty} \frac{X^{n}}{n!}
= I + \frac{X}{1!} + \frac{X^{2}}{2!} + \frac{X^{3}}{3!} + \cdots因此:
e^{-i \theta X}
= I + \frac{-i \theta X}{1!} + \frac{(-i \theta X)^{2}}{2!} + \frac{(-i \theta X)^{3}}{3!} + \cdots对于自反算符 A,有:
\begin{aligned}
e^{-i \theta A}
&= I + \frac{-i \theta A}{1!} + \frac{(-i \theta A)^{2}}{2!} + \frac{(-i \theta A)^{3}}{3!} + \cdots \\[4pt]
&= I - \frac{i \theta A}{1!} - \frac{\theta^2 A^{2}}{2!} + \frac{i \theta^3 A^{3}}{3!} - \frac{\theta^4 A^{4}}{4!} + \cdots \\[4pt]
&= I\left( 1 - \frac{\theta^2}{2!} + \frac{\theta^4}{4!} - \frac{\theta^6}{6!} + \cdots \right)
- iA\left( \frac{\theta}{1!} - \frac{\theta^3}{3!} + \frac{\theta^5}{5!} - \frac{\theta^7}{7!} + \cdots \right) \\[4pt]
&= I \cos\theta - i A \sin\theta
\end{aligned}Pauli 门
对于 X 门:
X = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}为自反矩阵:
X^2 = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} = I因此有:
e^{-i \theta X} = I \cos\theta - i X \sin\theta当 θ = π 是,有:
\begin{aligned}
R_x(\pi)
&= e^{-i \frac{\pi}{2} X} \\
&= I \cos\frac{\pi}{2} - i X \sin\frac{\pi}{2} \\
&= I \cdot 0 - i X \cdot 1 \\
&= -i X
\end{aligned}由于 -i 为全局相位因子,对量子态的物理性质没有影响,因此有:
X \propto R_x(180^\circ)
即,Pauli-X 门在布洛赫球上对应的操作是使量子绕 x 轴旋转 180 度。
同理易得:Pauli-Y 门和 Pauli-Z 门分别在布洛赫球上对应的操作是使量子绕 y 轴和 z 轴旋转 180 度。
H 门(Hadamard 门)
对应 H 门:
\frac{1}{\sqrt{2}}\begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}的旋转轴 n 为:
\begin{aligned}
\hat{\sigma}_{n}
&= n_{x} \hat{\sigma}_{x} + n_{y} \hat{\sigma}_{y} + n_{z} \hat{\sigma}_{z} \\[4pt]
&= \tfrac{1}{\sqrt{2}} \hat{\sigma}_x + 0 \cdot \hat{\sigma}_y + \tfrac{1}{\sqrt{2}} \hat{\sigma}_z \\[4pt]
&= \tfrac{1}{\sqrt{2}}
\left(
\begin{bmatrix}
0 & 1 \\[2pt]
1 & 0
\end{bmatrix}
+
\begin{bmatrix}
1 & 0 \\[2pt]
0 & -1
\end{bmatrix}
\right) \\[8pt]
&= \tfrac{1}{\sqrt{2}}
\begin{bmatrix}
1 & 1 \\[2pt]
1 & -1
\end{bmatrix} \\[4pt]
&= H
\end{aligned}同时,H 门为自反算符:
H^2 = \left( \tfrac{1}{\sqrt{2}} \right)^{2}\begin{bmatrix}1 & 1 \\1 & -1\end{bmatrix}\begin{bmatrix}1 & 1 \\1 & -1\end{bmatrix} = \tfrac{1}{2}\begin{bmatrix}(1+1) & (1-1) \\(1-1) & (1+1)\end{bmatrix} =\begin{bmatrix}1 & 0 \\0 & 1\end{bmatrix}= I因此:
\begin{aligned}
R_n(\pi)
&= e^{-i \frac{\pi}{2} H} \\
&= I \cos\frac{\pi}{2} - i H \sin\frac{\pi}{2} \\
&= I \cdot 0 - i H \cdot 1 \\
&= -i H
\end{aligned}由于 -i 为全局相位因子,对量子态的物理性质没有影响,因此有:
H \propto R_n(180^\circ)
倍数旋转
因为
\big(R_{\hat n}(\theta)\big)^{x} = e^{-i \frac{\theta}{2} \, \hat{\sigma}_{n} \, x} = e^{-i \frac{x\theta}{2} \, \hat{\sigma}_{n}} = R_{\hat n}(x\theta)即,对任意旋转算符取 x 次方,相当于将原来的旋转角度乘以对应的倍数 x。这里的倍数 x 可以是任意实数:当 0<x<1 时,表示部分旋转;当 x<0 时,表示反向旋转(角度取负)。
需要特别指出的是,将“旋转门的 x 次方”等同为“将旋转角乘以 x”是精确成立的,并且不会引入额外的全局相位,因为我们是在指数形式下直接运算。然而,当将旋转门与 Pauli 门(或其它矩阵)直接比较时,应注意可能存在的全局相位差异,这可能会影响两者的严格等价性,但不会影响物理可观测量。

发表回复