在量子计算和信息理论中,一个核心且基础的问题是如何处理量子信息。正如量子不可克隆原理(No-Cloning Theorem)所述,任何未知的、任意的量子态都不能被精确地复制(克隆)。
这意味着,不存在一个通用的酉操作 U 能够将一个初始状态未知的量子精确地转化为两个相同的相同的副本。
然而,尽管量子态不能被克隆,但它们可以被传输。量子隐形传态(Quantum Teleportation)是一种利用量子纠缠和经典通信,将一个量子比特的信息从发送方(Alice)转移到接收方(Bob)的技术。这个过程的关键在于:
- 传输是销毁性的,即为了将信息转移到目标量子比特上,原始量子比特的状态必须被破坏。
- 传输不是一个纯粹的量子操作,需要通过测量获得经典信息,用于对目标比特进行校正。
本文通过一个三量子比特的量子电路示例,详细分析量子隐形传态的矩阵形式及量子态演化过程,展示状态是如何被“销毁”和“重建”的。
初始状态设定
考虑三量子比特 q0,q1,q2,初始状态为:
\begin{aligned}
\ket{q_0} &= \alpha \ket{0} + \beta \ket{1} \\
\ket{q_1} &= \ket{0} \\
\ket{q_2} &= \ket{0}
\end{aligned}我们希望将 q0 复制至 q2,q1 为中间变量,满足:
\alpha, \beta \in \mathbb{C}, \quad |\alpha|^2 + |\beta|^2 = 1初始电路
对于设计如下的量子电路:
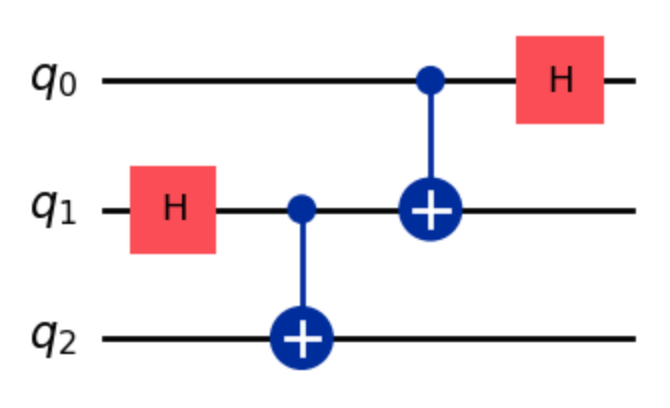
有:
\begin{aligned}\mathit{circuit} &= (H \otimes I \otimes I) \cdot (CX \otimes I) \cdot (I \otimes CX) \cdot (I \otimes H \otimes I) \\
&=\frac{1}{2}\begin{bmatrix}1&0&1&0&0&1&0&-1\\0&1&0&1&1&0&-1&0\\0&1&0&-1&1&0&1&0\\1&0&-1&0&0&1&0&1\\1&0&1&0&0&-1&0&1\\0&1&0&1&-1&0&1&0\\0&1&0&-1&-1&0&-1&0\\1&0&-1&0&0&-1&0&-1\end{bmatrix}\end{aligned}量子态演化
将电路作用于初始状态,得到:
\begin{aligned}
\text{circuit} \ket{q_0 q_1 q_2}
&= \text{circuit} (\ket{q_0} \otimes \ket{q_1} \otimes \ket{q_2}) \\
&=
\frac{1}{2}\begin{bmatrix} \alpha \\ \beta \\ \beta \\ \alpha \\ \alpha \\ -\beta \\ -\beta \\ \alpha \end{bmatrix} \\
&=\frac{1}{2} (\alpha \ket{000} + \beta \ket{001} + \beta \ket{010} + \alpha \ket{011} \\
&\quad + \alpha \ket{100} - \beta \ket{101} - \beta \ket{110} + \alpha \ket{111}) \\
&=\frac{1}{2} ( \ket{00} (\alpha\ket{0} + \beta\ket{1}) + \ket{01} (\beta\ket{0} + \alpha\ket{1}) \\
&\quad + \ket{10} (\alpha\ket{0} - \beta\ket{1}) + \ket{11} (-\beta\ket{0} + \alpha\ket{1}))
\end{aligned}此时,量子 q0 的信息已经高度纠缠地分散在 q0、q1 和 q2 上了。 此时,q2 尚未成为 q0 的副本。
经典通信与状态重建
为了完成传输与状态重建,必须对 q0 和 q1 进行测量,并基于测量结果对 q2 施加对应的校正操作,从而重建 q2 为 q0 的相同状态:
\begin{aligned}
\alpha\ket{0} + \beta\ket{1} &\longrightarrow I\\
\beta\ket{0} + \alpha\ket{1} &\longrightarrow X\\
\alpha\ket{0} - \beta\ket{1} &\longrightarrow Z\\
-\beta\ket{0} + \alpha\ket{1} &\longrightarrow ZX
\end{aligned}测量与销毁:q0 状态崩塌
对 q0 和 q1 的状态进行测量。根据测量结果,总态会坍缩到四个基底态之一:00、01、10 或 11,这导致了量子传态过程需要通过测量获得经典信息,且无法克隆产生相同状态量子。
经典校正
如前所述,坍塌基底态对 q2 施加相应矫正,从而使 q2 恢复到和 q0 相同的状态,从而实现从 q0 到 q2 的量子状态传输:
U_\rho =
\begin{cases}
I, & \rho = 00\\
X, & \rho = 01\\
Z, & \rho = 10\\
ZX, & \rho = 11
\end{cases}不难发现,这里的四种情况可以根据 q0 和 q1 的测量值使用控制门实现:
\mathit{CX}_{12} \otimes \mathit{CZ}_{02}至此,最终电路图为:
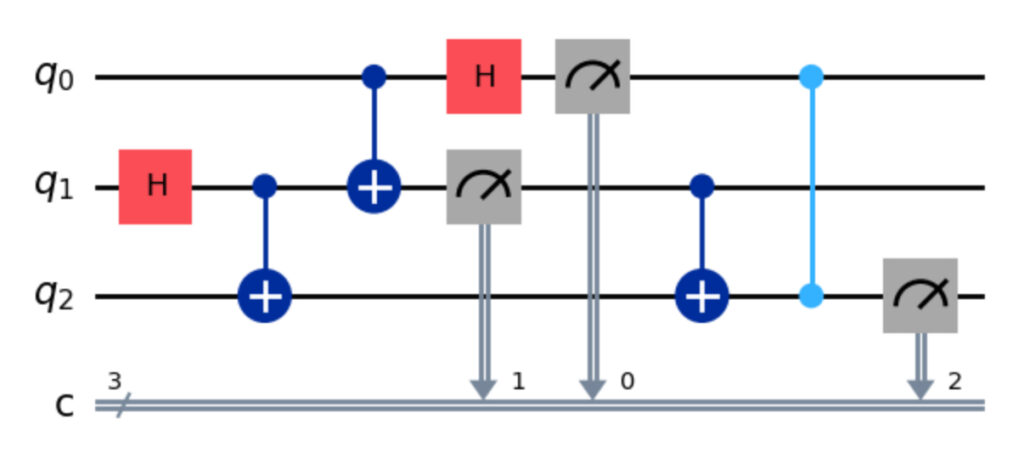
对应的 Qiskit 代码为:
qc = QuantumCircuit(3, 3)
#任意 qc.u(0)
qc.h(1)
qc.cx(1,2)
qc.cx(0,1)
qc.h(0)
qc.measure([0,1], [0,1])
qc.cx(1,2)
qc.cz(0,2)
qc.measure([2],[2])
发表回复